Write the program to arrange the n queen(queen of chessboard) in n*n matrix such that they can not ATTACK TO eachother.

 OUTPUT: In form of matrix of elements (0 and 1)

    where 1 is suitable position where can be keep without attack to each other.

  USED : Recursion , BACKTRACKING etc

CHARACTERISTICS OF QUEEN:

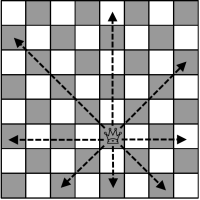
    A)They can move in any position in a row where it is presence.

    B)They can move in any position in a column where it is presence.

    C)They can move in any position in a diagonal where it is presence.

CONDITION:
    Arrange the queen such that they can not ATTACK to each other.
    in n*n matrix
   
  APPROCH:
   A )put a queen in a row than move next row to put
     the next queen in next row such that they can not ATTACK each other
      

After matrix 4 they are not any place where a queen can be
Put without attack by anyone so BACKTRACK occur here and reach again to
Matrix 1 and then continue to take step from steps to matrix 5 and again make continue to5 to matrix 8.

   
    B) after the puting the queen make that position  1 continue this by
      for_ putting  next queen send next position for_ checking suitable
      position i.e that positon where not get 1 in row ,column
     as well in diagoanl .
   
    C)after put the queen move in the next row by using
      recursion(remove 1 row).
   
    D)if_ we get not suitable position for_ keeping queen
       then take BACKTRACK  and change the position and continue this checking process for finding  suitable position 
 
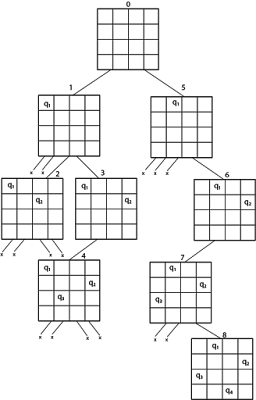
BACKTRAKING:Backtracking is a technique based on algorithm to solve problem.
      It uses recursive calling to find the solution by building a solution step by step increasing values with time.
      It removes the solutions that doesn't give rise to the solution of the problem based
  on the constraints given to solve the problem.
   
#include<iostream>
using namespace std;

bool isqueen(int** arr,int x,int y,int n)
{   
   /* To check that already
      queen is presence or not in the column */
    for(int row=0; row < x ; row++)
     {  if(arr[row][y]==1)
            {return false;}
            }
           
    //To check that already
    //  queen is presence or not in the first diogonal /
   
      int row=x;
      int col=y;
        while(row>=0 && col>=0)
            { if(arr[row][col]==1)
               {return false;}
           
            row--;
            col--;
           }
           
        row=x;
        col=y;      
       
   //To check that already
  //  queen is presence or not in the secound diogonal
    while(row>=0 && col<n)
            { if(arr[row][col]==1)
               {return false;}
           
                row--;
                col++;
            }
       
      return true;
   }  
        
       
  bool arrangequeen(int** arr ,int x,int n)
{   if( x >= n)
     {return true;}
   
    for(int col=0;col<n;col++)
      { if(isqueen( arr,x,col,n))
          {arr[x][col]=1;
        if(arrangequeen(arr,x+1,n))
         { return true;}
          arr[x][col]=0; // backtracking
          }
        }
              return false;
            }
           
int main()
{

  int n;
    cout<<"n ";
    cin>>n;
    int** arr = new int *[n];
     for(int i=0;i<n;i++)
    {arr[i]=new int[n];
   
   for(int j=0;j<n;j++)
        {arr[i][j]=0;}
       
     }  
       
        if(arrangequeen(arr,0,n))
        for(int i=0;i<n;i++)
    {for(int j=0;j<n;j++)
        {cout<<arr[i][j]<<" ";}
        cout<<endl;
        }
        return 0; }

 Click on below link and run this program

https://onlinegdb.com/r1T88tgL_